[数据结构]树
B树
- B树,又称多路平衡查找树。
B树中所有结点的孩子个树的最大值被称为B树的阶,通常用m表示。一棵m节的B树要么是空树,要么满足以下性质:
- 每个结点,之多有m棵子树,即至多含m-1个关键字
- 若根结点非终端结点,则至少有两棵子树。
- 除根结点外,所有非叶子结点至少有⌈m/2⌉,即至少含有⌈m/2⌉-1个关键字
- 所有叶子结点都出现在同一层次上,并不带信息(即NULL)。即绝对平衡
经典的B树(4阶)如下图所示:
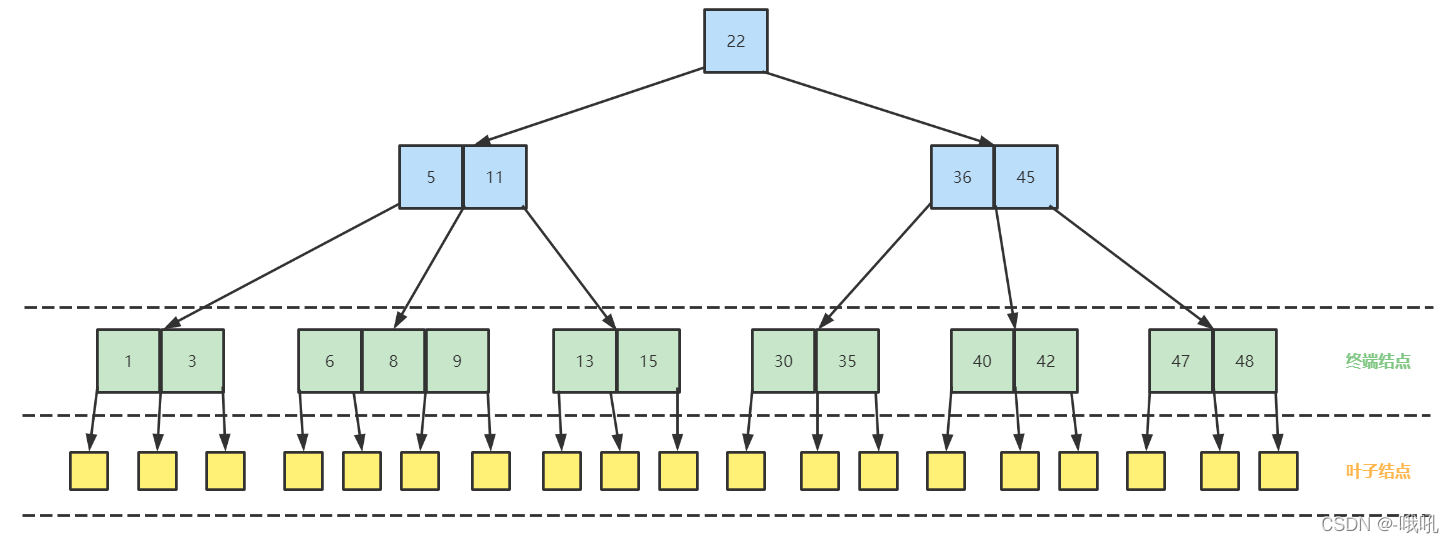
查找过程
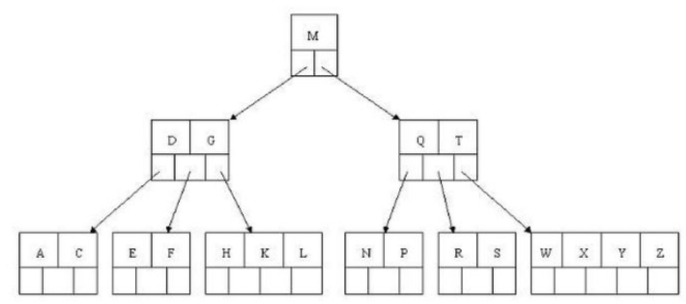
如上图要找到E。
- 1.从根节点的关键字进行比较,当前根节点为M,E < M ,所以找到指向左边的子节点。
- 2.拿到关键字D和G,D < E < G 所以直接找到D和G的中间结点
- 3.拿到E和F,找到E直接返回关键字和指针信息。
插入
针对m阶高度h的B树,插入一个元素时,首先在B树中是否存在,如果不存在,则在终端结点中插入该新的元素。
- 若该结点元素个数小于m-1个,直接插入;
- 若该结点元素个数等于m-1,引起结点分裂;以该结点总监元素为分界,取中间元素(偶数个数,中间两个随机选取)插入到父结点中。
- 重复上面动作,知道所有结点符合B树规则;最坏的情况一直分裂到根节点,生成新的根节点,高度+1.
B+树
虽然B树的查找效率十分优秀,但有一个缺陷。
- 数据库中的数据都是啊找记录存放的,每条记录都是由多个数据项组成。一次每条数据记录一般会很长。
- 如果我们使用B树,那么每个节点将存储的内容就是记录本身,B树将记录本身作为单位存放。
- 比如我们用一个5阶B树组织在校学生的数据记录,那么我们阶段都至少存储2条学生记录。
- 但是在检索的过程中,由于每个结点所占据的存储很大,我们实际的检索速度很难像前面展示的那些B树一样实现快速的检索(前面的树中每个结点的数据记录都是关键字本身,非常小)。
因此我们引入了B+树。
- B+树的特殊之处在于它将我们的记录的内容放在了叶子节点上。
- 其他节点和终端结点只存放关键字。
- 同时所有的结点的关键字都会啊自此出现在该关键字对应的子节点上。即所有的关键字都会出现在终端结点上,这样保证了每个叶子结点上的数据记录都能够有一个关键字于其对应。
- 这样的调整下我们每个结点之需要存放记录对应关键字,由此相较于B树,在同样大小的结点约束下,我们的B+树的每个结点可以存放更多的关键字,从而大幅度降低我们的树高,提升检索速度。
- 在B树的基础上将从m个关键字对应m+1个分支变成了m个关键字对应m个分支,即B+树的结点最大关键字数与B+数的阶相同。
B+树的基本性质
一棵m阶的B+树需要满足下列条件:
- 1.每个分支结点最多有m棵树和m个关键字。
- 2.根节点至少两棵子树,其他每个分支结点至少有⌈m/2⌉棵子树。
- 3.结点的子树个数与关键字个数相等。
- 4.每个关键字都应该出现在其对于子节点中,且每个结点都按照从小到大顺序排列。
- 5.所有终端结点包含全部关键字及只想相应记录的指针。同时终端结点将关键字从小到大顺序排列,并且终端结点按大小顺序相互链接起来。
- 6.同样是绝对平衡的。
其树形(4阶B+树)如下图所示: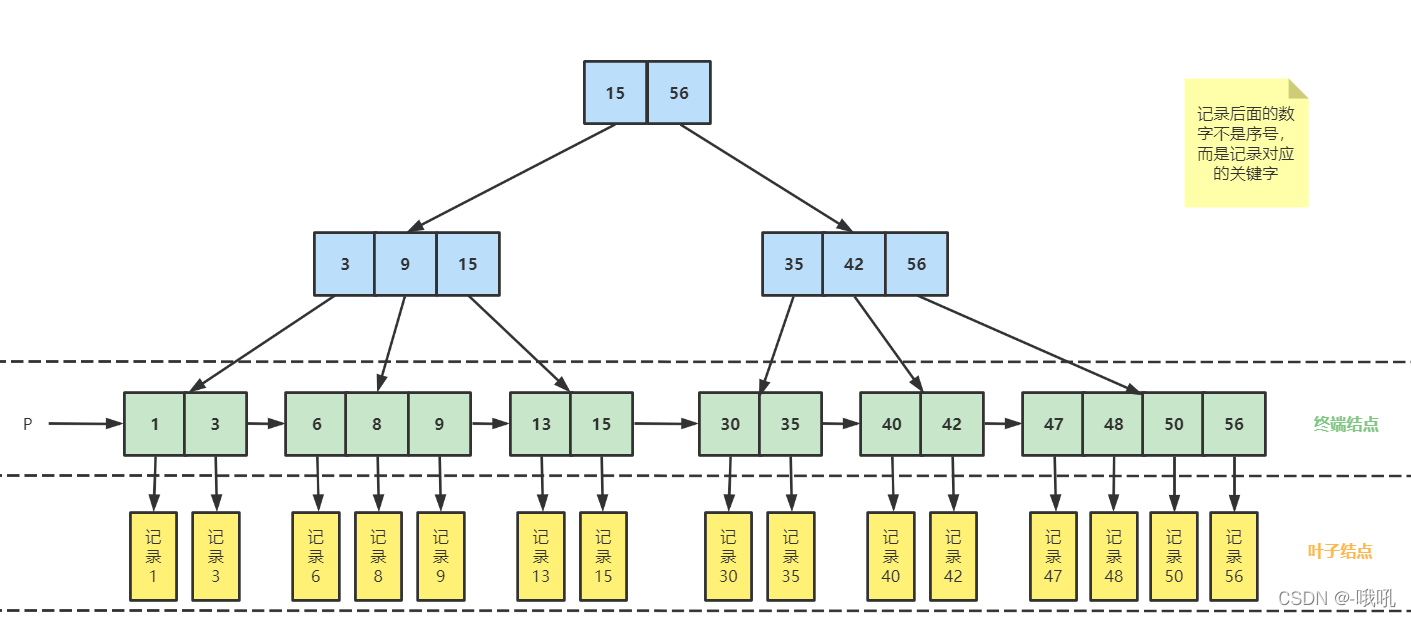
B+树的查找
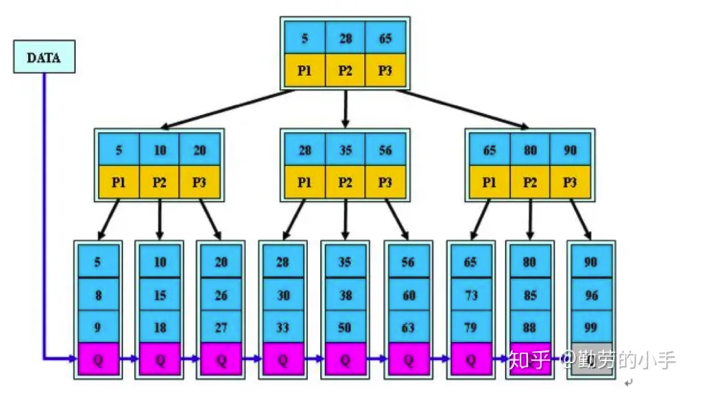
与分快查找类似。
- 从根节点出发,从节点中的关键字进行顺序遍历,每个关键字是其对应子树中的最大关键字
- 因此,若前一个关键字小雨目标关键字,而后一个大于目标关键字,则访问后一个关键字对应的子树,不断循环这个过程,直到终端结点就可以找到对应的数据记录了。
B树与B+树的区别
- 1.结点结构不同:
- B树的结点中除了包含关键字和对应的指针外,还包含了所有子节点的指针。
- B+树的节点只包含关键字和对应的指针,子节点的指针存储在叶子节点中。
- 2.叶子节点不同:
- B树的叶子节点存储了所有的数据记录。
- B+树的叶子及诶单只存储了关键字和对应的指针,数据记录存储在叶子节点对应的数据块中,然后沿着叶子节点的脸白哦一次查找数据记录。
- 3.叶子节点的顺序不同:
- B树中叶子节点没有顺序。
- B+树中,所有叶子节点都按照关键字顺序存储,形成了一个有序的序列,方便范围查询。
- 4.插入和删除操作不同:
- B树中,插入和删除操作需要进行节点的分类和合并,保证树的平衡性。
- B+树中,插入和删除的操作只需要修改叶子节点,并且不需要进行平衡操作,因为叶子节点之间的顺序关系已经保证了树的平衡性。
B+树的优势
- B+树层级更少:相较于B树,B+树每个非叶子节点存储的关键字树更多,树的层级更少所以查询数据更快。
- B+树查询速度相对稳定:B+树所有关键字数据地址都存在叶子节点砂锅,所以每次查找的次数相同,查询速度稳定。
- B+树天然具备排序功能:B+树所有的叶子节点数据构成了一个有序链表,在查询大小区间的数据时候更方便,数据紧密性很高,缓存的命中率也会比B树高。
- B+树全节点遍历更快:B+树遍历整棵树只需要遍历所有的叶子节点即可,,而不需要像B树一样需要对每一层进行遍历,这有利于数据库做全表扫描。
打个比方:B+树就有点像我们的目录,是索引的一个形式。若一个目录中,除了每个章节的名称外还需包含每章的大致内容,那么本来一页就可以看完的目录就会变成很多也,这并不方便我们从中去找到我们所需要的内容。
红黑树
红黑树是一种自平衡二叉查找树。具有良好的平衡性和高效的查找,插入、删除擦偶作。
- Java中的TreeMap类和TreeSet类都是基于红黑树实现的。
- TreeMap类是一种有序的Map接口实现,他的健值对按照健的自然顺序或者指定顺序进行排序。
- TreeSet类是一种有序Set接口实现,他按照元素的自然顺序或者指定比较器顺序进行排序。
- 这些类在插入、删除和查找元素时,都利用了红黑树的自平衡性质,使得操作的时间复杂为O(logn)
- Java中的ConcurrentSkipListMap类和ConcurrentSkipListSet类也是基于红黑树实现的。这些类通过对红黑树的操作进行加锁来保证线程安全性。
- Java中的PriorityQueue类也是基于堆实现的,而堆又可以使用红黑树实现。PriorityQueue类是一种优先级队列,它支持插入元素、删除最小元素等操作,并且能保证最小元素总是在队首。在Java中,PriorityQueue类的是基于小根堆的,但也可以使用红黑树来实现。
- 总之,红黑树在Java中被广泛运用于实现有序集合、优先级队列等数据结构。
红黑树不严格要求高度差不能超过1,而是需要满足5个规则:
- 1.每个节点可以时黑色或是红色。
- 2.根节点一定是黑色。
- 3.红色节点的父节点和子节点不能为红色,也就是说不能有两个连续的红色。
- 4.所有的空间点都是黑色(空节点视为NIL,红黑树中将空节点视为叶子节点)。
- 5.每个节点到空节点(NIL)路径上处在的黑色节点个树都相等。
例子:
- 一开始只有一个根节点,根节点必须是黑色的,所以直接变成黑色。
现在要插入一个新的节点,所有新插入的节点,默认情况下是红色。

新来的节点7根据规则直接放在11的左边就行了。
- 7的左右两边都是NULL,默认都是黑色,图中未画。
右边也插入一个节点:

继续插入:

插入节点4后,发现违反了规则3,因为红色结点的父结点和子结点不能为红色,此时为了保持以红黑树的性质,我们就需要进行颜色变换才可以。
只需要直接将父节点和其兄弟节点同时修改为黑色(为啥兄弟结点也需要变成黑色?因为要满足性质5),然后爷爷节点变成红色即可:

需要注意,因为爷爷节点正常情况下会变成红色,相当于新来了个红色的。
- 这时还需要继续往上看有没有破坏红黑树的规则才可以,知道没有为止。
比如这里破坏了性质一,爷爷节点现在是根节点(不是根节点就需要管),必须是黑色,所以要把它改成黑色。
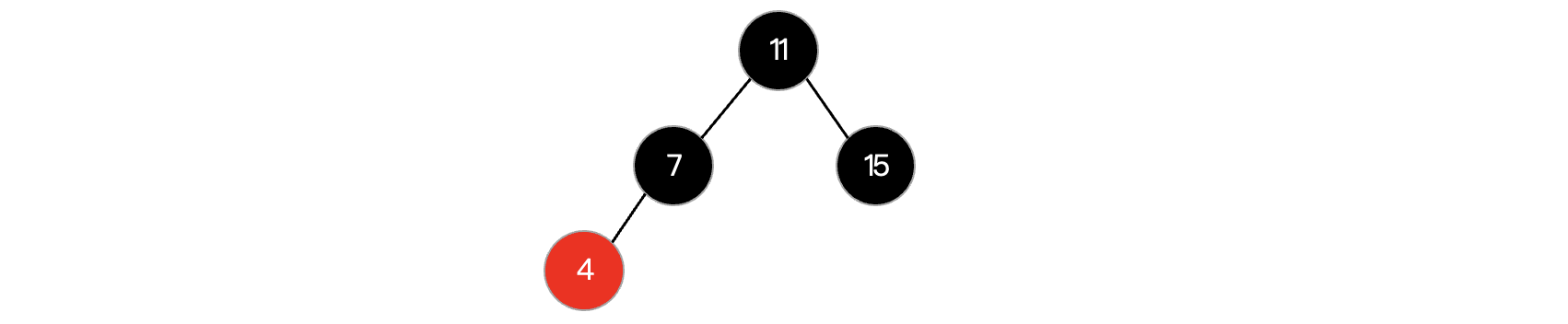
接着继续插入结点:
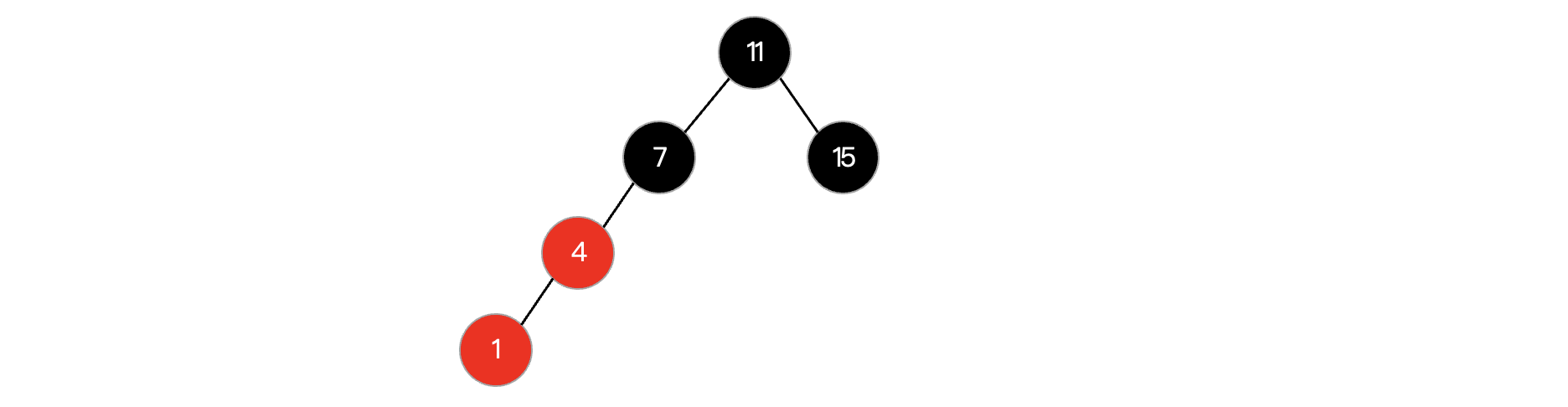
此时有两个红色的结点,我们需要进行变色。
但发现如果我们变色,那么从11开始到所有NIL结点经历的黑色结点数量就不对了:
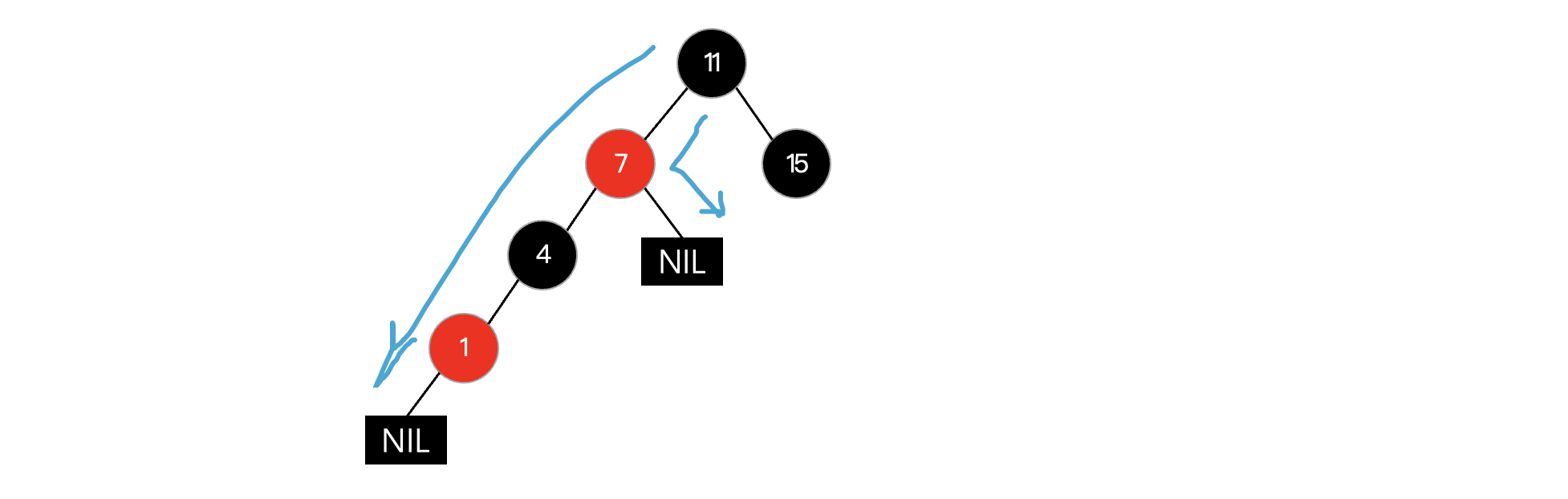
所以说对于这种父结点为红色,父结点的兄弟结点为黑色(NIL视为黑色)的情况,变色无法解决问题了。
我们只能考虑旋转了,旋转规则和我们之前讲解的平衡二叉树是一样的,这实际上是一种LL型失衡:
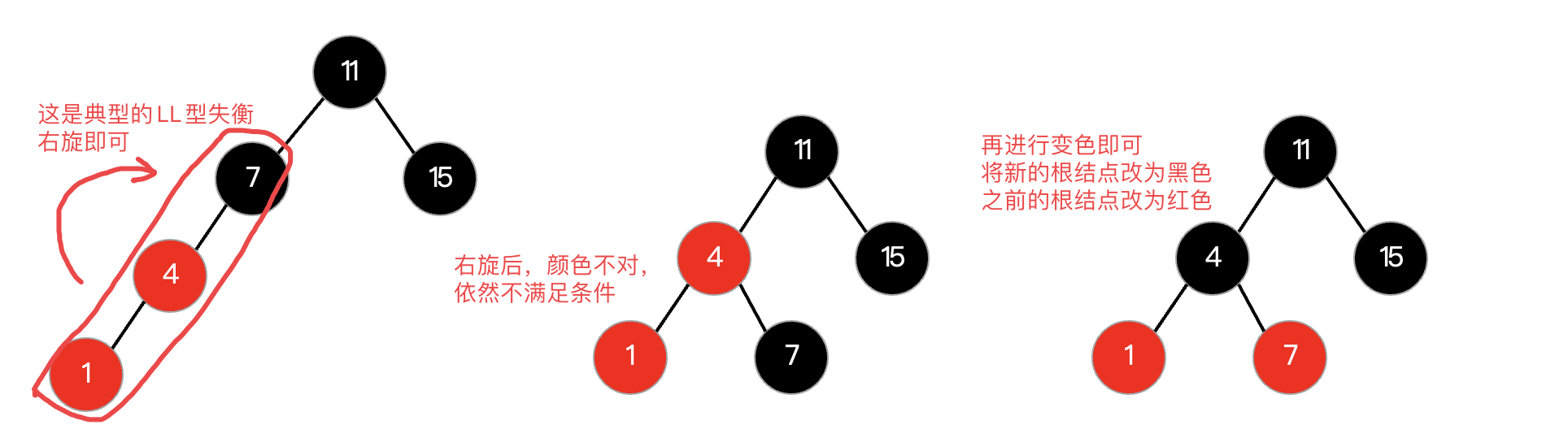
同样的,如果遇到了LR型失衡,跟前面一样,先左旋在右旋,然后进行变色即可:
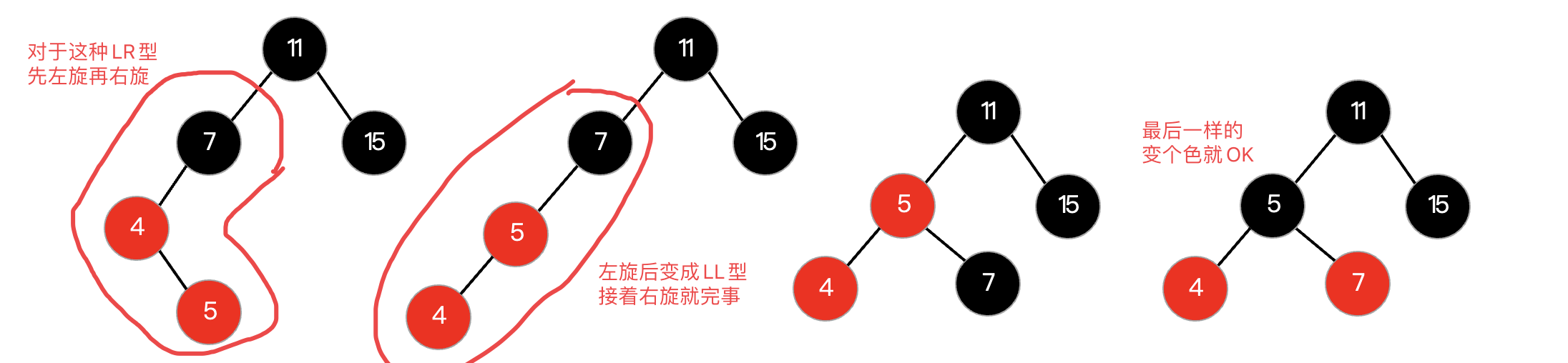
而RR型和RL型同理,这里就不进行演示了,可以看到,红黑树实际上也是通过颜色规则在进行旋转调整的,当然旋转和变色的操作顺序可以交换。
- 所以,在插入时比较关键的判断点如下:
- 如果整棵树为NULL,直接作为根节点,变成黑色。
- 如果父节点是黑色,直接插入。
- 如果父节点是红色,且父节点的兄弟节点也是红色,直接变色。(但是注意得继续往上看有没有破坏之前的结构)
- 如果父节点是红色,其兄弟节点为黑色,需要先根据情况(LL、RR、LR、RL)进行旋转,然后再变色。